Masalah
pengurutan merupakan persoalan yang menarik, karena terdapat puluhan algoritma
pengurutan yang pernah dikemukakan orang. Tidak semua algoritma pengurutan akan
dibahas di dalam postingan kali ini, hanya beberapa pengurutan sederhana yang akan
dijelaskan. Pengurutan (sorting)
adalah proses mengatur sekumpulan objek menurut urutan atau susunan terntentu.
Pengurutan
dapat dilakukan secara urut naik (ascending) maupun urut turun (descending).
Contoh
data angka :
20
|
13
|
17
|
19
|
15
|
11
|
18
|
16
|
12
|
14
|
Jika
diurutkan secara menaik (ascending) :
11
|
12
|
13
|
14
|
15
|
16
|
17
|
18
|
19
|
20
|
Jika
diurutkan secara menurun (descending) :
20
|
19
|
18
|
17
|
16
|
15
|
14
|
13
|
12
|
11
|
Berikut
adalah beberapa metode pengurutan dalam algoritma :
1. Insertion Sort
Salah
satu algoritma sorting yang paling sederhana adalah insertion sort. Insertion
Sort disebut-sebut sebagai metode pertengahan. Artinya, metode ini memiliki
kecepatan rata-rata antara metode primitif (bubble dan selection) dan modern
(merge dan quick). Metode ini, didasarkan pada sebuah kunci yang diambil pada
elemen ke-2 pada sebuah larik, lalu menyisipkan elemen tersebut jika kondisi
percabangan terpenuhi. Metode penyisipan (insertion) bertujuan untuk menjadikan
bagian sisi kiri larik terurutkan sampai dengan seluruh larik berhasil
diurutkan.
Ide dari algoritma ini dapat
dianalogikan seperti mengurutkan kartu. Penjelasan berikut ini
menerangkan bagaimana algoritma insertion sort bekerja dalam pengurutan kartu.
Misalkan sebuah array bertipe integer berisi angka-angka sebagai berikut :
3
|
0
|
1
|
8
|
7
|
2
|
5
|
4
|
9
|
6
|
Jika data diatas diurutkan secara menaik (ascending)
menggunakan metode insertion sort maka prosesnya sebagai berikut :
3
|
0
|
1
|
8
|
7
|
2
|
5
|
4
|
9
|
6
|
Pada perulangan ke-1 data pada array indeks ke 1 dijadikan
sebagai data sisip, kemudian dibandingkan dengan data yang ada sebelumnya, jika
data sebelumnya ada yang lebih besar dari data sisip maka ada data yang harus
digeser ke arah kiri, sekarang data sisip digeser satu tempat ke tempat paling
depan.
0
|
3
|
1
|
8
|
7
|
2
|
5
|
4
|
9
|
6
|
Pada perulangan ke-2 data pada array indeks ke 2 dijadikan
sebagai data sisip, kemudian dibandingkan dengan data yang ada sebelumnya, jika
data sebelumnya ada yang lebih besar maka data sisip harus digeser ke arah
kiri, sekarang data sisip berada pada array indeks ke 1.
0
|
1
|
3
|
8
|
7
|
2
|
5
|
4
|
9
|
6
|
Pada perulangan ke-3 data pada array indeks ke 3
dijadikan sebagai data sisip, kemudian dibandingkan dengan data yang ada
sebelumnya, jika data sebelumnya tidak ada yang lebih besar dari data sisip maka
tidak ada data yang harus bergeser.
0
|
1
|
3
|
8
|
7
|
2
|
5
|
4
|
9
|
6
|
Pada perulangan ke-4 data pada array indeks ke-4
dijadikan sebagai data sisip, kemudian dibandingkan dengan data yang ada
sebelumnya, terdapat data yang nilainya lebih besar dari data sisip maka data
sisip harus bergeser ke arah kiri, sekarang data sisip berada pada array indeks
ke-4.
0
|
1
|
3
|
7
|
8
|
2
|
5
|
4
|
9
|
6
|
Pada perulangan ke-5 data pada array indeks ke-5
dijadikan sebagai data sisip, kemudian dibandingkan dengan data yang ada
sebelumnya, terdapat tiga data yang lebih besar nilainya dari data sisip, maka
data sisip itu harus digeser. Sekarang data sisip berada pada array indeks
ke-2.
0
|
1
|
2
|
3
|
7
|
8
|
5
|
4
|
9
|
6
|
Pada perulangan ke-6 data pada array indeks ke-5
dijadikan sebagai data sisip, data sisip kemudian dibandingkan dengan data yang
ada sebelumnya, terdapat dua data yang nilainya lebih besar dari data sisip,
maka data sisip itu harus digeser. Sekarang data sisip berada pada array indeks
ke-4.
0
|
1
|
2
|
3
|
5
|
7
|
8
|
4
|
9
|
6
|
Pada perulangan ke-7 data pada array indeks ke-6
dijadikan sebagai data sisip, kemudian, data sisip dibandingkan dengan data
yang ada sebelumnya, terdapat tiga data yang nilainya lebih besar dari data
sisip, maka data sisip itu harus digeser. Sekarang data sisip berada pada array
imdeks ke-4.
0
|
1
|
2
|
3
|
4
|
5
|
7
|
8
|
9
|
6
|
Pada perulangan ke-8 data pada array indeks ke-8
dijadikan sebagai data sisip, kemudian dibandingkan dengan data yang ada
sebelumnya, jika data sebelumnya tidak ada yang lebih besar dari data sisip
maka tidak ada data yang harus bergeser.
0
|
1
|
2
|
3
|
4
|
5
|
7
|
8
|
9
|
6
|
Pada perulangan ke-9 data pada array indeks ke-9
dijadikan sebagai data sisip, kemudian data sisip dibandingkan dengan data yang
ada sebelumnya, terdapat tiga data yang memiliki nilai lebih besar dari data
sisip maka data sisip harus bergeser. Sekarang data sisip berada pada array
indeks ke-6.
Hasil akhir :
0
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
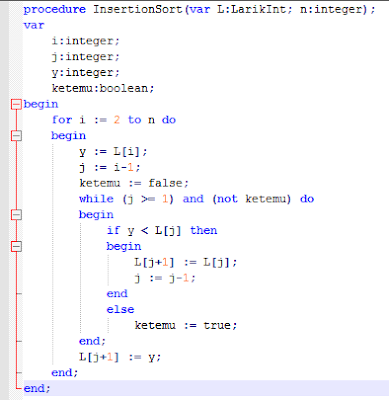
Implementasi Bahasa Pascal
Implementasi Bahasa C
2.
Metode Gelembung (Bubble Sort)
Algoritma Bubble Sort
ini merupakan proses pengurutan yang secara berangsur-angsur berpindah ke
posisi yang tepat karena itulah dinamakan Bubble yang artinya gelembung.
Algoritma ini akan mengurutkan data dari yang terbesar ke yang terkecil (ascending) atau sebaliknya (descending).
Secara
sederhana, bisa didefenisikan algoritma Bubble Sort adalah pengurutan
dengan cara pertukaran data dengan data disebelahnya secara terus menerus
sampai dalam satu iterasi tertentu tidak ada lagi perubahan.
Untuk belajar algoritma Bubble Sort
ini kita hanya perlu memahami cara yang digunakan untuk mengurutkan data,
sederhananya algoritma ini menggunakan perbandingan dalam operasi antar
elemennya. Di bawah ini merupakan gambaran dari algoritma Bubble Sort dengan
array “4 2 5 3 9”.
Proses pertama
(4 2 5 3 9) menjadi (1 3 5 3 9)
(2 4 5 3 9) menjadi (1 3 5 3 9)
(2 4 5 3 9) menjadi (1 3 3 5 9)
(2 4 3 5 9) menjadi (1 3 3 5 9)
(4 2 5 3 9) menjadi (1 3 5 3 9)
(2 4 5 3 9) menjadi (1 3 5 3 9)
(2 4 5 3 9) menjadi (1 3 3 5 9)
(2 4 3 5 9) menjadi (1 3 3 5 9)
Proses kedua
(2 4 3 5 9) menjadi (2 4 3 5 9)
(2 4 3 5 9) menjadi (2 3 4 5 9)
(2 3 4 5 9) menjadi (2 3 4 5 9)
(2 3 4 5 9) menjadi (2 3 4 5 9)
(2 4 3 5 9) menjadi (2 4 3 5 9)
(2 4 3 5 9) menjadi (2 3 4 5 9)
(2 3 4 5 9) menjadi (2 3 4 5 9)
(2 3 4 5 9) menjadi (2 3 4 5 9)
Proses ketiga
(2 3 4 5 9) menjadi (2 3 4 5 9)
(2 3 4 5 9) menjadi (2 3 4 5 9)
(2 3 4 5 9) menjadi (2 3 4 5 9)
(2 3 4 5 9) menjadi (2 3 4 5 9)
(2 3 4 5 9) menjadi (2 3 4 5 9)
(2 3 4 5 9) menjadi (2 3 4 5 9)
(2 3 4 5 9) menjadi (2 3 4 5 9)
(2 3 4 5 9) menjadi (2 3 4 5 9)
Jika kita perhatikan proses diatas,
para proses kedua data sudah terurut dengan benar. Tetapi algoritma Bubble Sort
tetap berjalan hingga proses kedua berakhir. Proses ketiga masih terus berjalan
karena pada algoritma Bubble Sort maksud terurut itu adalah tidak ada satupun
penukaran pada suatu proses. Proses ketiga ini dilakukan untuk verifikasi data.
Algoritma Bubble Sort ini mempunyai
kelebihan dan kekurangan, untuk kelebihannya metode ini merupakan metode paling
sederhana untuk mengurutkan data. Selain sederhana, algoritma Bubble Sort mudah
dipahami. Sementara itu, kekurangannya terletak pada efisiensi.
Bubble Sort ini merupakan metode
pengurutan yang tidak efisien karena ketika mengurutkan data yang sangat besar
akan sangat lambat prosesnya. Selain itu, jumlah pengulangan akan tetap sama
jumlahnya meskipun data sudah cukup terurut.
Implementasi Bahasa Pascal
Implementasi Basaha C
3.
Metode Shell Sort
Alogoritma
pengurutan Shell diberi nama sesuai
nama penemunya (Donald Shell tahun 1959). Algoritma ini merupakan perbaikan
terhadap metode pengurutan sisip. Kelemahan metode pengurutan sisip sudah
disebutkan pada bagian sebelumnya. Jika data pada posisi ke-1000 ternyata
posisi yang tepat adalah sebagai elemen kedua, maka dibutuhkan kira-kira 998
kali pergeseran elemen.
Untuk
mengurangi pergeseran terlalu jauh, kita menurutkan larik setiap k elemen
dengan metode pengurutan sisip, misalkan kita urutkan setiap 5 elemen (k kita
namakan juga step atau increment).
Selanjutnya, kita gunakan nilai step yang lebih kecil, misalnya k = 3, lalu
kita urut setiap 3 elemen. Begitu seterusnya sampai nilai k = 1. Karena nilai
step selalu berkurang maka algoritma pengurutan Shell kadang-kadang dinamakan
jua algoritma pengurutan kenaikan yang berkurang (diminishing increment sort).
Proses pengurutan dengan Shell sort dapat
disimulasikan sebagai berikut:
Pertama menentukan jarak mula-mula dari data yang akan
dibandingkan, yaitu N/2. Data pertama dibandingkan dengan data dengan jarak
N/2. Apabila data pertama lebih besar dari data ke N/2 tersebut maka kedua data
tersebut ditukar. Kemudian data kedua dibandingkan dengan jarak yang sama yaitu
N/2. Demikian seterusnya sampai seluruh data dibandingkan sehingga semua data
ke-j selalu lebih kecil daripada data ke-(j + N/2).
Pada proses berikutnya, digunakan jarak (N/2) / 2 atau
N/4. Data pertama dibandingkan dengan data dengan jarak N/4. Apabila data
pertama lebih besar dari data ke N/4 tersebut maka kedua data tersebut ditukar.
Kemudian data kedua dibandingkan dengan jarak yang sama yaitu N/4. Demikianlah
seterusnya hingga seluruh data dibandingkan sehingga semua data ke-j lebih
kecil dari data ke-(j + N/4).
Pada proses berikutnya, digunakan jarak (N/4) / 2 atau
N/8. Demikian seterusnya sampai jarak yang digunakan adalah 1.
Algoritma metode Shell dapat dituliskan sebagai
berikut :
1.
Jarak = N
2.
Selama (Jarak > 1)
kerjakan baris 3 sampai dengan 9
3.
Jarak = Jarak / 2. Sudah =
false
4.
Kerjakan baris 4 sampai
dengan 8 selama Sudah = false
5.
Sudah = true
6.
j = 0
7.
Selama (j < N – Jarak)
kerjakan baris 8 dan 9
8.
Jika (Data[j] > Data[j +
Jarak] maka tukar Data[j], Data[j + Jarak], Sudah = true
9.
j = j + 1
Implementasi Bahasa Pascal
Daftar Pustaka :
Munir, Rinaldi. 2013. Algoritma & Pemrograman dalam Bahasa Pascal dan C Edisi Revisi. Bandung : Informatika.
Analisis Aloritma Insertion Sort, Merge Sort, Arief Hendra Saptaji
Baca juga :







0 komentar:
Posting Komentar